光子气体
参考书籍《热物理概念 热力学与统计物理学》
1 电磁辐射的经典热力学
我们将环境视为体积为V 的容器(在这个主题中它称为“空窖”),温度维持为T.
窖内的光子与窖壁达到热平衡,形成电磁驻波.如图23.1所示,窖壁由可以导热的材料组成(即窖壁可以在窖内的光子气体和环境之间传输热量)
如果n为窖中光子气体单位体积的光子数,则气体的能量密度u可以写成
$$u=\frac{U}{V}=n\hslash\omega\tag{1}$$
其中$\hslash\omega$是一个光子的平均能量.从动理学理论(之后写)可知,粒子气体的压强为$P=\frac{1}{3}nm<v^2>$. 对于光子,用光速的平方$c^2$取代该公式中的$<v^2>$.
将$mc^2$解释为一个光子的能量,则有辐射压强p等于能量密度的1/3.于是
$$p=\frac{u}{3}\tag{2}$$
它不同于气体动理学理论中的表示式($p=\frac{2u}{3}$)
(2)给出了电磁辐射产生的辐射压强的表示式.
又由动理学理论可知,在容器壁上光子的通量$\Phi$,也就是说每秒钟撞击容器壁单位面积的光子数,由下式给出:
$$\Phi=\frac{1}{4}nc\tag{3}$$
其中c是光速.(但更应该为$\frac{\mathrm{d}\Phi}{\mathrm{d}t}=\frac{1}{4}nc$,但为了和其他章一致还是保留原书$\Phi$的写法)
由该式与方程(1),我们可以将光子产生的单位窖壁面积上的入射功率写为
$$F=\hslash w\Phi=\frac{1}{4}uc\tag{4}$$
当我们现在推导斯特藩- 玻尔兹曼定律(Stefan-Boltzmann law)时,这个关系将是非常重要的.
斯特藩-玻尔兹曼定律将物体的温度T与由它辐射的、呈现为电磁辐射形式的能量通量联系起来.我们可以用形式为$\mathrm{d}U=T\mathrm{d}S-p\mathrm{d}V$的热力学第一定律推导出这个关系.
第一定律给出
$$(\frac{\partial U}{\partial V})_{T}=T(\frac{\partial S}{\partial V})_{T}-p=T(\frac{\partial p}{\partial T})_{V}-p\tag{5}$$
其中最后一个等式使用了麦克斯韦关系.
方程(5)的左边就是能量密度u.因此,利用方程(5)以及方程(2),可以得到
$$u=\frac{1}{3}T(\frac{\partial u}{\partial T})_{V}-\frac{u}{3}\tag{6}$$
整理得
$$4u=T(\frac{\partial u}{\partial T})_{V}\tag{7}$$
由此则有
$$4\frac{\mathrm{d}T}{T}=\frac{\mathrm{d}u}{u}\tag{8}$$
对方程(8)积分可得
$$u=AT^4\tag{9}$$
其中,$A$是积分常数,单位为$J\cdot K^{-4}\cdot m^{-3}$.现在用方程(4)可以得到单位面积上的入射功率为
$$F=\frac{1}{4}uc=(\frac{1}{4}Ac)T^4=\sigma T^4\tag{10}$$
其中括号中的项$\sigma =\frac{1}{4}Ac$是斯特藩-玻尔兹曼常量(Stefan-Boltzmann constant).
方程(10)称为斯特藩- 玻尔兹曼定律(Stefan-Boltzmann law)或有时称为斯特藩定律(Stefan’s law).
现在还不清楚常量$\sigma$取什么值,这是起初由实验确定值的某个量.在后面中,利用统计力学的方法我们可以导出这个常量的一个表示式.
2 谱能量密度
我们继续应用经典的处理方法,看看这种方法能达到什么程度.
为此,考虑两个容器,每一个均与温度为T的热源接触,两个容器之间通过一个管子相连,如图23.2所示,允许系统可以达到平衡.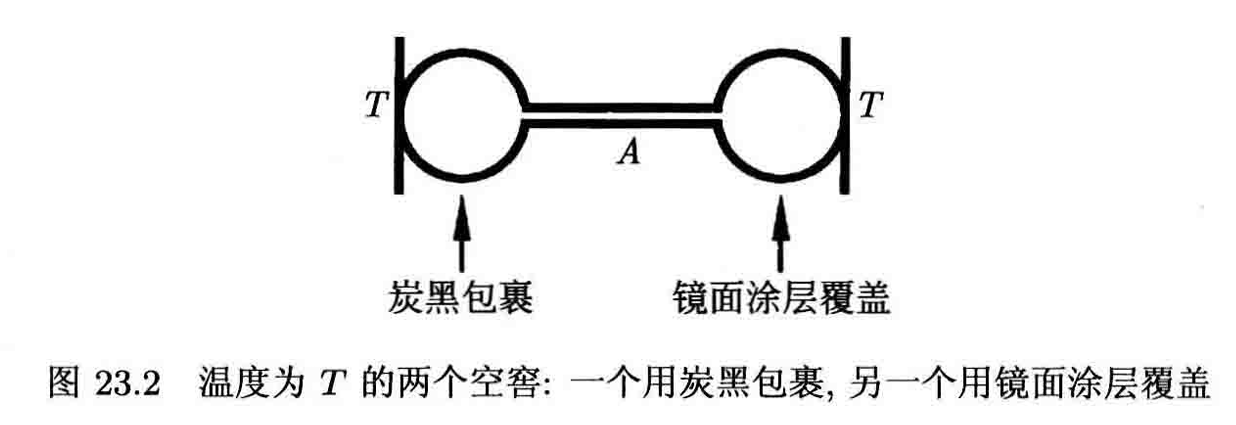
两个热源处于相同的温度T,所以由热力学第二定律可知,不可能有净的热量从一个物体流到另一个物体.
因此,沿着管子不可能有净的能量通量,所以从用炭黑包裹的空窖沿着管子由左到右的能量通量与从用镜面涂层覆盖的空窖由右到左的能量通量必定相平衡.
于是,由方程(9)可知,两个空窖必有相同的能量密度u.这个论证可以对不同形状、大小以及不同涂层的空窖重复进行.因此我们可以得出结论,能量密度微与空窖的形状、大小或者空窖的材料无关.
但是,尽管两个空窖总体上有相同的能量密度,是否可能在某些波长下,一个空窖的能量密度比另一个更大呢?情况不是如此,如我们现在将证明的.
首先,我们作一个定义.
谱能量密度(spectral energy density)$u_\lambda$可定义如下:$u_\lambda\mathrm{d}\lambda$是波长位于$\lambda$和$\lambda+\mathrm{d}\lambda$之间的那些光子的能量密度.于是,总的能量密度为
$$u=\int u_\lambda\mathrm{d}\lambda\tag{11}$$
现在假设有一个滤波器,它只允许在波长$\lambda$附近一个窄的辐射波带通过,将它插在图23.2中的A 处,并使系统达到平衡.
上面列出的相同论证在这种情况下仍然适用:空窖之间没有净的能量通量,因此在一个很窄的波长范围内每个空窖的比内能是相同的,即
$$u_\lambda^\text{炭黑}{ ( T ) }=u_\lambda^\text{镜面}{ ( T ) }\tag{12}$$
这表明光谱内能和空窖的材料、形状、大小或者性质无关.因此谱能量密度仅仅是$\lambda$和$T$的一个普适函数.
3 基尔霍夫定律
我们现在希望讨论一个空窖的特殊表面将会怎样吸收或辐射具有特定频率或波长的电磁辐射.
因此,我们作下面几个另外的定义:
谱吸收率(spectral absorptivity)$\alpha_\lambda$表示物体对波长为$\lambda$的入射辐射吸收的百分比;
表面的谱辐射功率(spectral emissive power)$e_\lambda$是一个函数,它使得$e_\lambda\mathrm{d}\lambda$表示波长位于$\lambda$与$\lambda+\mathrm{d}\lambda$之间的电磁辐射每单位面积的辐射功率.
利用这些定义,我们现在可以写出表面每单位面积吸收功率的形式.如果入射谱能量密度$u_\lambda\mathrm{d}\lambda$,则吸收功率为
$$(\frac{1}{4}u_\lambda\mathrm{d}\lambda c)\alpha_\lambda\tag{13}$$
表面每单位面积的辐射功率为
$$e_\lambda\mathrm{d}\lambda\tag{14}$$
在平衡状态下,方程(13)和方程(14)这两个表示式必定是相等的,因此有
$$\frac{e_\lambda\mathrm{d}\lambda}{\alpha_\lambda}=\frac{c}{4}u_\lambda\tag{15}$$
方程(15)是基尔霍夫定律(Kirchhoff’s law)的表示式,它指出比值$\frac{e_\lambda\mathrm{d}\lambda}{\alpha_\lambda}$是$\lambda$和$T$的一个普适函数.
因此,如果我们固定$\lambda$和$T$,则比值$\frac{e_\lambda\mathrm{d}\lambda}{\alpha_\lambda}$就固定了,因此有$e_\lambda\propto\alpha_\lambda$换言之, “良好的吸收体是良好的辐射体”以及“不好的吸收体是不好的辐射体.”
一个理想的黑体(black body)定义为一个对于所有波长$\lambda$均有$\alpha_\lambda=1$的物体.根据方 程(15)所表示的基尔霍夫定律,我们知道对于$\alpha$的这个最大值,黑体是可能的最好辐射体.
常常最有用的是考虑黑体空窖(black body cavity),它是一个腔,其壁对于所有波长$\lambda$均有$\alpha_\lambda=1$,并且由于壁中的原子发射和吸收光子,空窖内包含了与壁有相同温度的光子气体.
包含在黑体空窖中的光子气体称为黑体辐射(black body radiation).